Вот и первая задача в этом блоге.
Все мы с детского садика знаем, как разделить отрезок на две равные части с помощью циркуля и линейки. А вот как разделить отрезок пополам, пользуясь ТОЛЬКО циркулем (без линейки)?
Решение
Дан отрезок AB, требуется разделить его пополам с помощью циркуля.
Построение
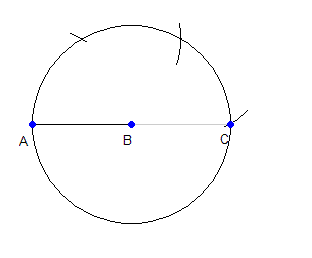
Шаг 1. Проведём окружность радиуса AB с центром в точке B. Тем же раствором циркуля отмерим на этой окружности три дуги, начиная от точки A. Получим точку C.
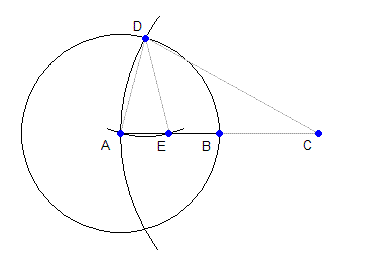
Шаг 2. Проведём окружность радиуса AB с центром в точке A и окружность радиуса AC с центром в точке C. Одну из точек пересечения этих окружностей обозначим D.
Шаг 3. Проведём окружность радиуса AB с центром в точке D. Она пересечёт отрезок AB в точках A и E, причём точка E делит отрезок AB пополам.
Доказательство
Очевидно, что точка C лежит на прямой AB, причём AB=BC, т.е. AC=2*AB
По построению треугольники ACD и ADE - равнобедренные, поэтому углы DAE, AED и ADC равны. Отсюда следует, что треугольники ACD и ADE подобны.
Запишем отношения сторон: AE/AD = AD/AC, следовательно AE = AD*AD/AC = AB*AB / (2*AB) = AB/2.
Доказательство закончено.
Этим методом можно делить отрезок не только на 2, но и на N частей. Более того, с незначительными модификациями этот метод применим в случае, когда исходный отрезок вообще не проведён (т.е. заданы только его концы).
Все мы с детского садика знаем, как разделить отрезок на две равные части с помощью циркуля и линейки. А вот как разделить отрезок пополам, пользуясь ТОЛЬКО циркулем (без линейки)?
Решение
Дан отрезок AB, требуется разделить его пополам с помощью циркуля.
Построение
Шаг 1. Проведём окружность радиуса AB с центром в точке B. Тем же раствором циркуля отмерим на этой окружности три дуги, начиная от точки A. Получим точку C.
Шаг 3. Проведём окружность радиуса AB с центром в точке D. Она пересечёт отрезок AB в точках A и E, причём точка E делит отрезок AB пополам.
Очевидно, что точка C лежит на прямой AB, причём AB=BC, т.е. AC=2*AB
По построению треугольники ACD и ADE - равнобедренные, поэтому углы DAE, AED и ADC равны. Отсюда следует, что треугольники ACD и ADE подобны.
Запишем отношения сторон: AE/AD = AD/AC, следовательно AE = AD*AD/AC = AB*AB / (2*AB) = AB/2.
Доказательство закончено.
Этим методом можно делить отрезок не только на 2, но и на N частей. Более того, с незначительными модификациями этот метод применим в случае, когда исходный отрезок вообще не проведён (т.е. заданы только его концы).
Хм... почему точка C лежит на прямой AB? Либо я не понимаю построение, либо она там не лежит.
ОтветитьУдалитьНе могу сообразить, как вставить рисунок в комментарий, поэтому объясню словами.
ОтветитьУдалитьНа шаге 1, откладывая от точки A три дуги раствором циркуля AB, мы получаем точки X, Y и C. По построению треугольники ABX, XBY и BYC - равносторонние, все их углы составляют 60 градусов.
Соответственно, угол ABC составлен из трёх углов по 60 градусов, т.е. является развёрнутым углом.
Все понял, спасибо!
ОтветитьУдалитьНе могли бы Вы показать, как разделить пополам дугу, а не отрезок
ОтветитьУдалить